Expressed as L = λW where L represents the average number of items, λ the average arrival rate per unit of time, and W the average waiting time, Little's Law provides a powerful tool for understanding and optimizing workflow in Kanban.
Let's illustrate the power of Little's Law with a practical example: a busy coffee shop. Imagine customers forming a queue to order and receive their coffee. During a specific hour, we observe the following: an average of 10 customers are present in the shop, either waiting in line or for their order. Furthermore, the average time a customer spends in the shop, from joining the line to receiving their drink, is 5 minutes. Using Little's Law, we can easily calculate the customer arrival rate. With L (average number of customers) equal to 10 and W (average waiting time) equal to 5 minutes (or 1/12 of an hour), the calculation becomes λ = L/W, which is 10 divided by 1/12, resulting in 120 customers per hour. This indicates that, on average, 120 customers visit the coffee shop within that hour. This simple application of Little's Law provides valuable insights into customer flow, assisting in crucial decisions like staffing levels and the potential need for additional service counters to minimize wait times and reduce waste.

Regardless of its initial application in queuing theory, Little's Law proves remarkably versatile, extending to various systems and methodologies, including project and workflow management. Within project management, Little's Law adapts to focus on the system's departure rate, assuming a balance between average arrival and departure rates.
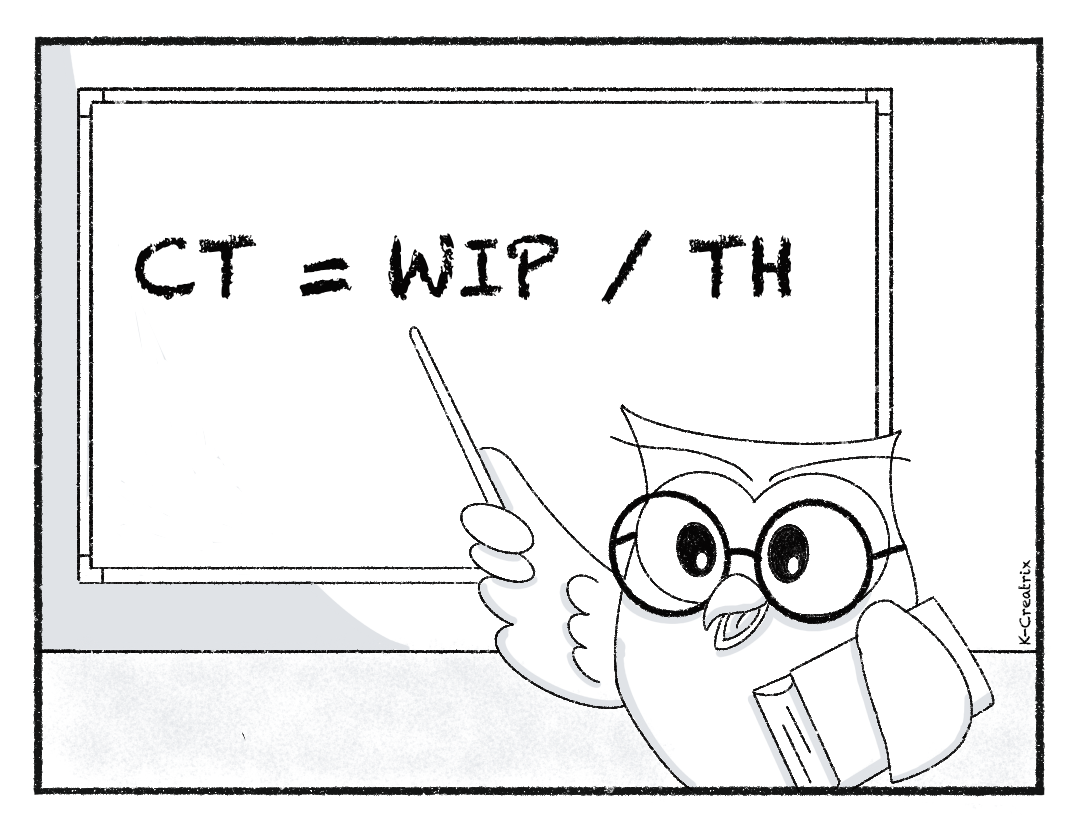
This leads to the formula: CT = WIP / TH
where CT represents the average Cycle Time, WIP is the average Work In Progress, and TH is the average Throughput, all measured over the same time period.
To see this in action, try a simple experiment. Using your tracked flow metrics, calculate your average Cycle Time, WIP, and Throughput for the past 60 days. Then, divide your average WIP by your average Throughput. You'll likely find that the result doesn't perfectly match your historical average Cycle Time.

The discrepancy between calculated and observed cycle times isn't a flaw in Little's Law itself, but rather an indication that your process isn't adhering to its fundamental assumptions. The Throughput version of Little's Law relies on five key conditions:
1. The average arrival rate must equal the average departure rate.
2. All items entering the workflow must eventually exit.
3. The Work In Progress (WIP) must remain stable, neither consistently increasing nor decreasing.
4. The average age of the WIP must also remain stable.
5. All measurements must be expressed in consistent units.
When your calculations don't align with your actual cycle time, it signifies a violation of one or more of these assumptions. This discrepancy is your cue to investigate your process. Are there existing policies that contradict these assumptions? Can you identify ad-hoc practices that disrupt the stability required by Little's Law? By examining your process through the lens of these assumptions, you can pinpoint areas for improvement, enhance predictability, and ultimately, optimize your workflow.

It's crucial to understand that Little's Law is a tool for retrospective analysis, not future prediction. As Dr. Little himself emphasised, it's about measurement, not forecasting. Therefore, attempting to use Little's Law to make deterministic predictions is a misapplication. The reason lies in the inherent unpredictability of future process variations. As we've seen, violations of Little's Law's assumptions, which can occur at any time, invalidate its predictive power. Instead, the true value of Little's Law lies in understanding its assumptions and shaping your process to align with them. When your workflow consistently adheres to these principles, your data becomes more reliable and your process becomes probabilistically predictable. At this point, you can leverage methods like Monte Carlo simulation on your historical data for forecasting with increased confidence. Little's Law helps you build a stable foundation for accurate probabilistic forecasting, but does not do the forecasting itself.

Source:
This post was inspired by Little's Law - Why You Should Care, guest writer Daniel Vacanti